unidades

Kibibytes, mebibytes e xibibytes

por

Sabemos que os dispositivos electrónicos dixitais traballan en lóxica binaria. É o caso,  por exemplo, dos procesadores dos nosos ordenadores e teléfonos móbiles ou os chips das calculadoras e reloxos dixitais. Todos estes trebellos utilizan coma unidade básica de información o bit (b), que pode valer 0 ou 1, segundo o estado lóxico da variable coa que se traballe.

Os rexistros dos primeiros procesadores que se popularizaron eran de 8 bits, polo que se adoptou o Byte (B) como unha unidade básica de almacenamento formada por un conxunto de 8 bits.

O problema chega ao facer os múltiplos. O Sistema Internacional de Unidades (SI) emprega como múltiplos das unidades o kilo (k 103), Mega (M 106),  Xiga (G 109), etc.

Ao traballar en binario obtemos números moi feos ao facer así os múltiplos. Por exemplo 1000= 103 en binario é 1111101000, e resultaba máis cómodo utilizar 1024= 210 (10000000000), polo que comezaron a utilizarse as equivalencias 1 kB = 1024 bytes ou 1 MB = 1024 kB.

Estas equivalencias aparecen en moitos textos de tecnoloxía, electrónica e informática. Incluso é común que alguén diga que un kilo equivale a 1000, agás en informática que equivale a 1024.

Isto é un erro. Faleivos moitas veces, especialmente en Bacharelato, da importancia que ten a normalización ou estandarización en Tecnoloxía. Estas normas serven para poder expresar e interpretar a información dunha maneira precisa e inequívoca, e non é admisible que un múltiplo se interprete de dúas formas diferentes. O Sistema Internacional é claro, e establece que un kilo é 1000 e non 1024.

Que facemos, entón, cos múltiplos binarios?

Para resolver isto e evitar confusións, desde 1998 o IEC (International Electrotechnical Commission) vén propoñendo outros prefixos para os múltiplos binarios: ki (kibi),  Mi (mebi),  Gi (xibi), cada un 1024 veces superior ao que lle precede, e que equivalen a kilobinario, megabinario e xigabinario respectivamente. (fonte)

Múltiplos binarios Múltiplos decimais
Nome Símbolo Factor Nome Símbolo Factor
kibi Ki (210)1 =210 kilo k (103)1 = 103
mebi Mi (210)2 = 220 mega M (103)2 = 106
xibi Gi (210)3 = 230 xiga G (103)3 = 109
tebi Ti (210)4 = 240 tera T (103)4 = 1012
pebi Pi (210)5 = 250 peta P (103)5 = 1015
exbi Ei (210)6= 260 exa E (103)6 = 1018

Á hora de medir a capacidade dos nosos soportes informáticos hai que ter coidado en como vén expresada. Non debemos sorprendernos se cando inserimos a nosa memoria USB de 2 GB o computador dinos que é de 1,95 GB, pois iso non significa que estea a facer mal as contas. O que sucede é que está chamando GB ao que en realidade son GiB.

Por exemplo, aquí podemos ver como nun sistema operativo GNU/Linux co escritorio KDE usa as medidas propostas polo IEC e converte unha memoria USB de 2GB (2 mil millóns de bytes) en 1,95GiB.

E aquí podemos ver como Windows XP non segue esta norma e chama GB ao que debería ser GiB.


Matemáticas co buscador de google

por

O buscador de google é, sen dúbida algunha, a máis eficaz ferramenta para facer procuras na web e atopar facilmente o que queremos. Pero non serve unicamente para iso. Sabías que o buscador de google funciona tamén como calculadora? Sabías que podemos utilizalo para a representación gráfica de funcións matemáticas? Sabías que con el podemos converter unidades?

Calculadora:

Para utilizalo como calculadora non hai máis que escribir na caixa de texto a operación que desexamos realizar e o resultado aparecerá ao darlle a buscar.

Os símbolos básicos con a suma +, resta -, multiplicación * e división /, pero hai outros:

Número “e” e e*1 = 2.71 Logaritmo base 10 log(nº) log(10) = 1
Número “pi” π pi 2*pi*4 = 25,13 Logaritmo neperiano ln(nº) ln(10) = 2.302
Exponencial ^  2^3 = 23= 8 Seno sin(nºrad) sin(pi/2)=1
Raíz cadrada sqrt(nº)  sqrt(2) = √2 Coseno cos(nºrad) cos(pi/2)=0
Factorial !(nº)  !4= 4·3·2·1 = 24 Tanxente tan(nºrad) tan(pi)=0

Podemos, ademais, utilizar diversas constantes físicas: G (gravitación universal), h (Planck), c (velocidade da luz no baleiro), etc.
 

Representación gráfica de funcións:

Unha das novidades máis recentes do buscador google é que permite a representación gráfica de funcións. Só temos que introducir a función que desexamos visualizar na caixa de texto do buscador e clicar en buscar.

Por exemplo, se introducimos sin(2e^x) o resultado é unha gráfica que podemos mover, ampliar e reducir. Ademais, vainos dicir as coordenadas do punto no que estea o cursor.

Tamén podemos debuxar varias funcións na mesma gráfica. Temos que escribilas separadas por unha coma e aparecerán representadas cada unha nunha cor diferente.


 

Conversor de unidades

Para utilizar o buscador de google como conversor de unidades temos que escribir o nome das unidades en inglés e separalas por “in” ou “to”.

  • 90 km/h to m/s → 25 meters/second
  • 30 Celsius in Fahrenheit → 86 degrees Fahrenheit
  • 5000 cal to J → 20 920 joules
  • 15 in to cm → 38.1 centimeters (in=polgada)

 

Conversor de sistemas de numeración

Tamén podemos utilizar o buscador para pasar dun sistema de numeración a outro.
Se o número que queremos converter está en binario hai que lle poñer “0b” diante, e se está en hexadecimal “0x”.

  • 45 in binary → 0b101101
  • 216 to hexadecimal → 0xD8
  • 0b1001 to decimal → 9
  • 0xf2 to decimal → 242
  • 2011 in roman numerals → MMXI

 

Realmente hai moitas máis cousas que podes facer co buscador de google. Bótalle unha ollada a esta páxina.


yocto, zepto, atto, femto … peta, exa, zetta, yotta

por

Podemos ter costume de traballar con picofaradios (1 pF = 10-12 F), megaohmios (1 MΩ = 106Ω) ou xigapascais (1 GPa = 109 Pa), pero hai outros prefixos que non soan moito xa que non os usamos, aínda que non está de máis coñecelos.

No Taller II temos un novo póster, unha adaptación informativa do póster que nos regalaron pola semana da Ciencia. Aquí tedes as equivalencias:

Prefixo Factor Símbolo yocto.jpg
yocto 10-24 y
zepto 10-21 z
atto 10-18 a
femto 10-15 f
pico 10-12 ?
nano 10-9 n
micro 10-6 µ
mili 10-3 m
centi 10-2 c
deci 10-1 d
deca 101 da
hecto 102 h
kilo 103 k
mega 106 M
xiga 109 G
tera 1012 T
peta 1015 P
exa 1018 E
zetta 1021 Z
yotta 1024 Y

Para entender o que significan estas dimensións vai dar unha volta polo interior do corpo humano, dun ordenador ou dun faro dun automóbil.
nanoreisen.jpg

(Este artigo forma parte da 1ª edición do entroido da física)


Medindo o Universo

por

Acabo de facer unha solicitude para acoller no insti a exposición “Medindo o Universo” do Laboratorio Oficial de Metroloxía de Galicia, anque non sei se seguirá funcionando este curso.

A exposición conta a historia da metroloxía e dos sistemas de unidades, contando con información válida para distintas áreas: Física e Química, Matemáticas, Tecnoloxía, Historia…

Os paneis pódense descargar en pdf

En 1º de bacharelato empezamos con exercicios de factores de conversión para coller soltura, e véxovos alucinando coa cantidade de unidades coas que se pode traballar, así que non está de máis coñecer un pouco de historia da metroloxía, cos seus problemas e retos.

medindo.png

Actualización 30/09/2010:
A exposición xa non está subvencionada, así que os centros que desexen expoñela deben asumir os gastos de transporte.


A importancia das unidades de medida

por

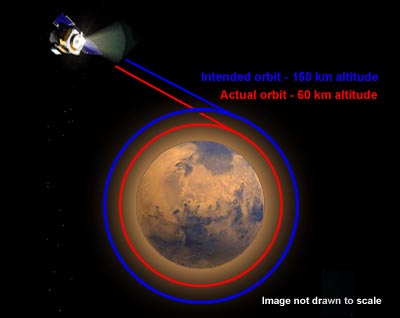MCO_OrbitQue pesados coas unidades! deben de pensar moitos alumnos e alumnas cando insistimos en que as indiquen correctamente. Pero é que non é para menos. Aquí vai un exemplo das consecuencias que pode ter non indicar correctamente as unidades de medida:

En setembro de 1999 a sonda espacial Mars Climate, enviada pola NASA para manterse na órbita de Marte e estudar o seu clima, estrelouse contra a súa superficie e quedou completamente estragada. Segundo fontes da NASA, o desastre debeuse a un erro nas unidades dos datos que se subministraron ao ordenador de abordo.

Resulta que na construción participaron empresas diferentes, e utilizáronse distintos sistemas de unidades para o deseño e construción da sonda espacial e para a programación dos sistemas de navegación. No primeiro caso os datos viñan expresados no sistema inglés de unidades (pés, millas, libras, …) mentres que no segundo caso utilizouse o Sistema Internacional de Unidades (S.I.) (metros, kilogramos, …)

Os datos e cálculos que fixo a empresa encargada do deseño da sonda espacial (sistema inglés) foron enviados á empresa encargada de programar os sistemas de navegación (que utiliza o Sistema Internacional), pero grave erro!, os datos enviáronse sen especificar as unidades de medida utilizadas, e a segunda empresa interpretounos como se estiveran expresados no S.I.. O resultado foi que os ordenadores da nave realizaron uns cálculos erróneos e situaron a nave nunha órbita equivocada, o que provocou o desastre.

Fonte: El rincón de la ciencia